# 算法复杂度

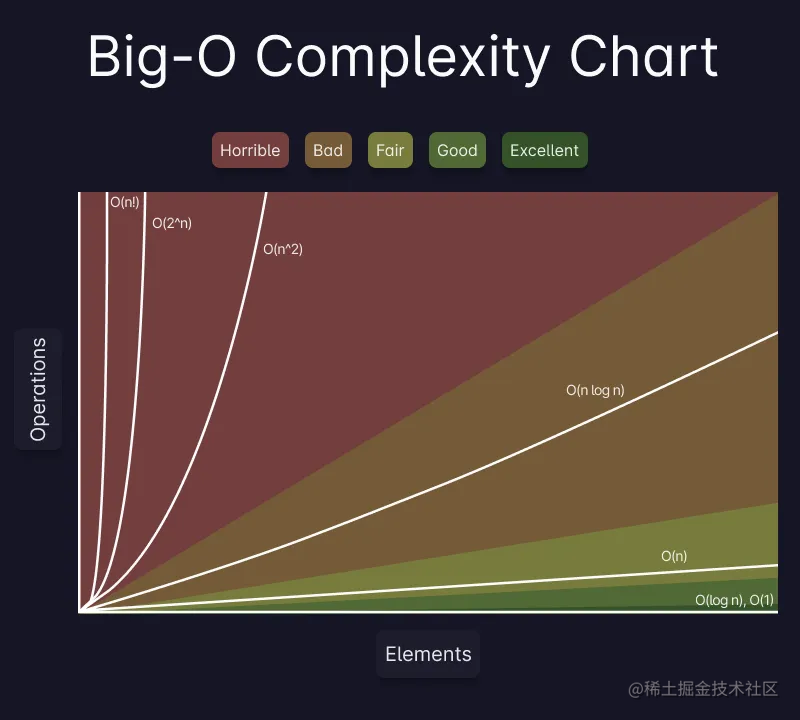
# O 的含义

我们一般使用大写O来表示算法的最坏情况下复杂度，我们一般它用来描述算法所需资源（如时间或者空间），它使用数学符号来描述算法复杂度与输入大小之间的关系。

不同的数据结构对同一操作具有不同的时间复杂度。一个常见的例子是链表具有O(1)时间复杂度的插入和删除操作，而同样操作数组的时间复杂度是O(n)。

# Ω(Omega) 和 Θ（Theta）

还有其他符号用于描述算法复杂度，如 Ω(Ωmega)和 Θ(Theta)。Ω 描述算法的最佳情况复杂度，而 Θ 描述算法的平均情况复杂度。

比如链表的插入和删除操作为Θ(1) 和 O(1)。还有常用数组排序算法的时间复杂度，如快速排序的最佳复杂度为Ω(n log n)，平均复杂度为Θ(n log n)和最坏复杂度为O(n^2)。

# 如何计算复杂度

这里只考虑时间复杂度，不考虑空间复杂度

要计算一个算法的复杂度，首先需要确定算法中最慢的部分，也就是瓶颈，这部分复杂度就是整个算法的复杂度。

通常来说，可以通过检查算法中所有的循环和递归操作，并计算它们运行的次数来确定瓶颈。每个循环或递归贡献一个计数，最终，我们取这些计数中最大的那一个作为算法复杂度。例如，如果算法中有两个循环，一个是 O(n)，另一个是 O(m)，那么算法的复杂度就是 O(max(n, m))。其中 n 和 m 分别代表数据的大小。

# 计算方法

算法复杂度的计算方法主要包括以下几种：

常数法则: 仅考虑最多的循环次数。
加法法则: 将算法中多个独立部分的时间复杂度相加。
乘法法则: 对于嵌套循环, 其时间复杂度是外层循环次数和内层循环次数之积。
大 O 记号法则: 只考虑算法中最高阶复杂度的项。

在计算复杂度的时候，应该尽量忽略常数，如果该算法中包含多个独立部分，则将它们的复杂度相加。

对于嵌套循环, 我们需要计算外层循环和内层循环的乘积.

# 举例说明

举一个常见的例子，O(1)，它表示常数时间复杂度，意味着算法所需时间与输入大小无关，并且是最高效的。比如：读取一个数组中的单个元素。因为访问数组中的单个元素是一个简单的操作，所以不需要遍历整个数组，只需要知道元素所在的位置即可。因此读取一个数组中的单个元素的时间复杂度是 O(1)。具体实现如下：
```
let arr = [1, 2, 3, 4, 5];
console.log(arr[3]); // 4
```

另外，O(n!)表示阶乘时间复杂度，这是最低效的，因为随着输入增长，资源增长很快。一个经典的例子是生成并打印全排列。

全排列算法的基本思想是递归地生成所有可能的排列，并在生成每种排列时进行递归。这种算法的时间复杂度是O(n!)，因为生成全排列需要进行n!次递归

function permute(arr) {
  function helper(current, remaining) {
    if (remaining.length === 0) {
      console.log(current);
      return;
    }
    for (let i = 0; i < remaining.length; i++) {
      helper(
        current.concat([remaining[i]]),
        remaining.slice(0, i).concat(remaining.slice(i + 1))
      );
    }
  }
  helper([], arr);
}

举一个时间复杂度是 O(n^2) 的例子

一个经典的例子是冒泡排序算法，冒泡排序的基本思想是重复地遍历序列，比较相邻的两个元素，如果它们的顺序错误就把它们交换过来。这个算法的时间复杂度是 O(n^2)，因为它需要进行 n 次外层循环和 n-1 次内层循环，总循环次数是 n*(n-1)这样就是 O(n^2)
```
function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}
```
举一个O(2^n)的例子 O(2^n)是指随着数据规模增大，算法运行时间的增长速度是指数级的。一个经典的例子是求解背包问题的递归算法。背包问题是这样的：给定n个物品和一个容量为V的背包，求如何让背包装入物品，使得装入物品的总价值最大。
```
function knapsack(weight, value, n, V) {
    if (n == 0 || V == 0) {
        return 0;
    }
    if (weight[n - 1] > V) {
        return knapsack(weight, value, n - 1, V);
    }
    return Math.max(
        value[n - 1] + knapsack(weight, value, n - 1, V - weight[n - 1]),
        knapsack(weight, value, n - 1, V)
    );
}
```
这个递归算法的时间复杂度是O(2^n)，因为每次调用都会让问题的规模翻倍，而算法会重复计