总体分三步

• 相同的前置节点和后置节点
• 判断是否需要进行 DOM 的移动
• 移动元素

第一部分 相同的前置节点和后置节点

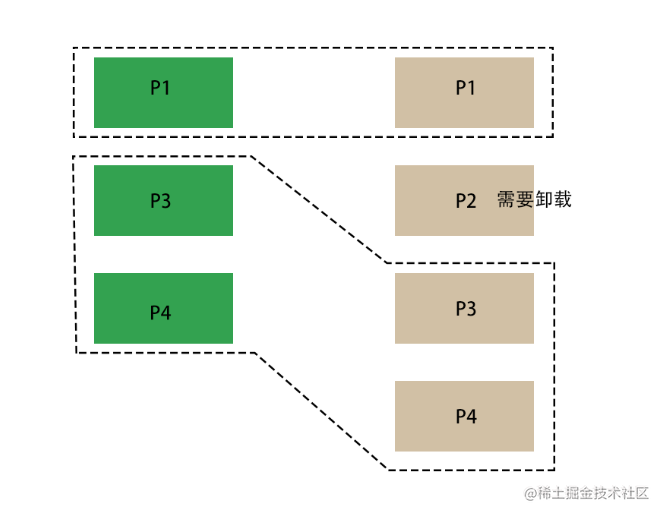
• 开启一个从头向尾的循环，判断 新旧节点的 key 是否相同，不相同退出
• 开启一个从尾向头的循环，判断 新旧节点的 key 是否相同，不相同退出
• 判断 新节点没有遍历完且旧节点遍历完，依次新增
• 判断 旧节点没有遍历完且新节点遍历完，依次卸载
• 判断 新节点没有遍历完且旧节点也没遍历完，则进行比较第二步部分（判断是否需要进行 DOM 的移动）

第二部分 判断是否需要进行 DOM 的移动

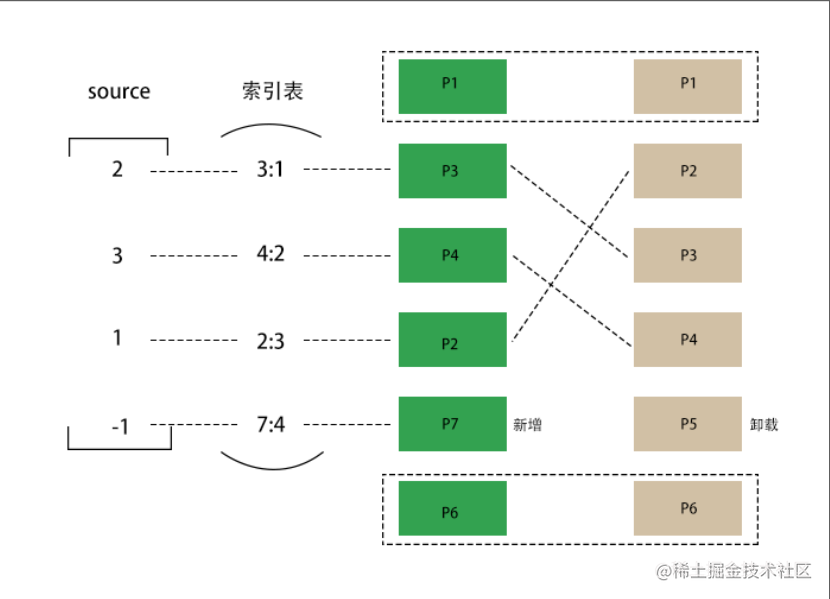
• 构建一个 sources 数组，用于存放，新节点对应旧节点组中的索引
  • 遍历新节点组，将其 el.key 作为[key],index 作为 [value] 保存为一个索引表
  • 遍历旧节点组，在索引表中找相同的 el.key
    • 没找到，卸载节点
    • 找到了，将其在旧节点中的索引 放入 索引的 source 中, 和简单 diff 算法类似，判断是否有需要移动的节点

第三部分 移动元素

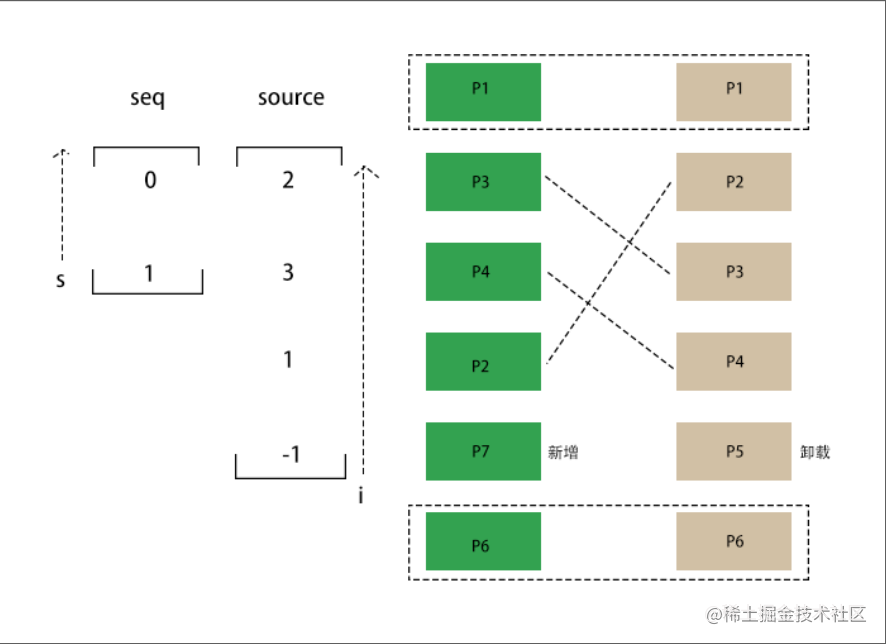
• 通过 source 计算出最长递增子序列 seq数组，表示最长递增子序列在source中的索引

最长递增子序列说明 这些节点的位置没有发生改变，可以不需要移动

• i 指向新的一组节点中的最后一个元素，· 指向最长递增子序列中的最后一个元素，循环使 i 递减，从下向上移动
  • 判断 i 是不是 -1 （-1 说明在节点中没有找到该新节点的位置），新增节点
  • 判断 i 和 seq[s] 不相等（说明该节点需要移动）
    • 找到该节点在新节点组中的真实位置作为锚点
    • 移动
  • 判断 i 和 seq[s] 相等，说明该节点不需要移动
    • s-- 向上继续

最长递增子序列

function getSequence(arr) {
  const p = arr.slice(); //  保存原始数据
  const result = [0]; //  存储最长增长子序列的索引数组
  let i, j, u, v, c;
  const len = arr.length;
  for (i = 0; i < len; i++) {
    const arrI = arr[i];
    if (arrI !== 0) {
      j = result[result.length - 1]; //  j是子序列索引最后一项
      if (arr[j] < arrI) {
        //  如果arr[i] > arr[j], 当前值比最后一项还大，可以直接push到索引数组(result)中去
        p[i] = j; //  p记录第i个位置的索引变为j
        result.push(i);
        continue;
      }
      u = 0; //  数组的第一项
      v = result.length - 1; //  数组的最后一项
      while (u < v) {
        //  如果arrI <= arr[j] 通过二分查找，将i插入到result对应位置；u和v相等时循环停止
        c = ((u + v) / 2) | 0; //  二分查找
        if (arr[result[c]] < arrI) {
          u = c + 1; //  移动u
        } else {
          v = c; //  中间的位置大于等于i,v=c
        }
      }
      if (arrI < arr[result[u]]) {
        if (u > 0) {
          p[i] = result[u - 1]; //  记录修改的索引
        }
        result[u] = i; //  更新索引数组(result)
      }
    }
  }
  u = result.length;
  v = result[u - 1];
  //把u值赋给result
  while (u-- > 0) {
    //  最后通过p数组对result数组进行进行修订，取得正确的索引
    result[u] = v;
    v = p[v];
  }
  return result;
}