前端小蜗

# 参数

  1. n1 - 旧的节点
  2. n2 - 新的节点
  3. container 挂载点

# 思路

  1. 循环遍历 比较
    1. 是否被处理过（6 中的非理想情况）。
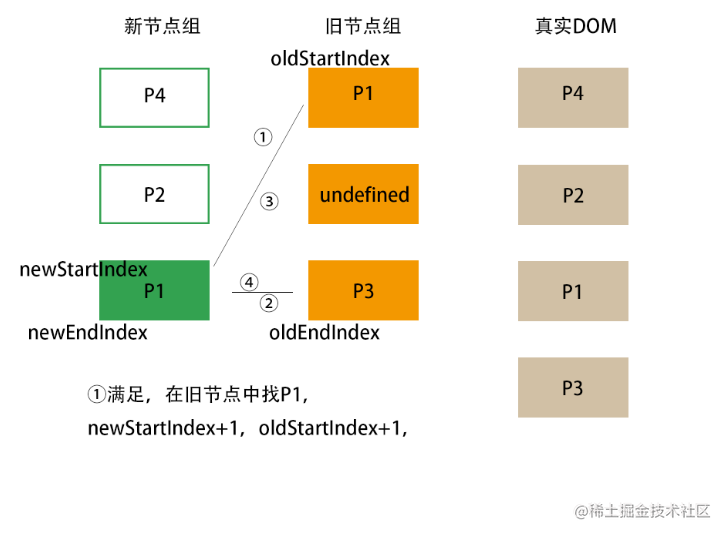
    2. 新首-旧首，打补丁，新首节点索引+1，旧首节点索引+1。
    3. 新尾-旧尾，打补丁，新尾节点索引-1，旧尾节点索引-1。
    4. 新尾-旧首，打补丁，旧首对应的 DOM 移动到旧尾节点的后面，新尾节点索引-1，旧首节点索引+1。
    5. 新首-旧尾，打补丁，旧尾对应的 DOM 移动到旧首节点的前面，新首节点索引+1，旧尾节点索引-1。
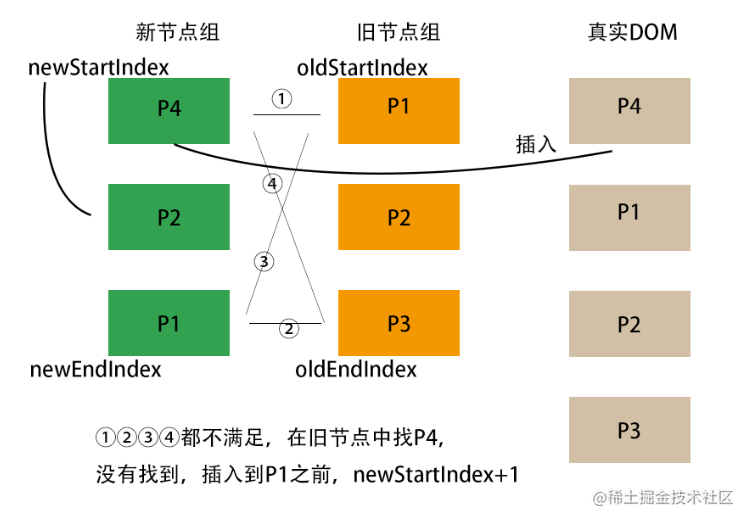
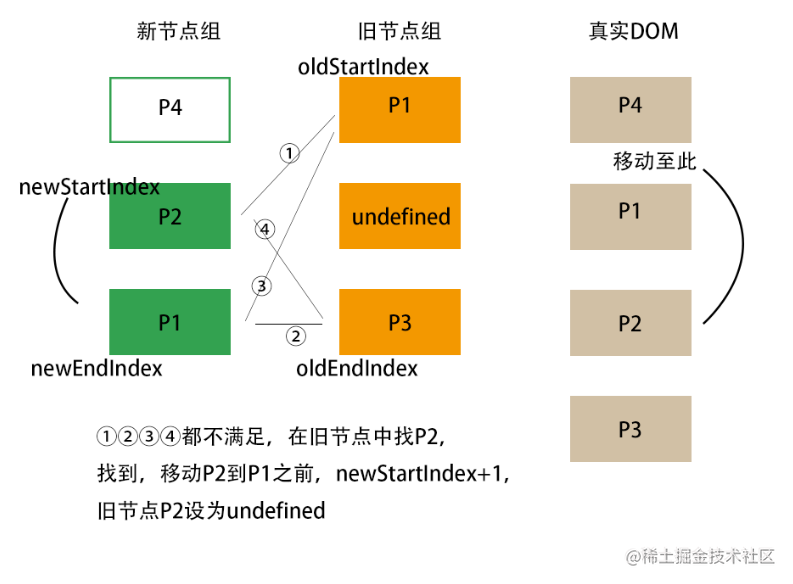
    6. 考虑非理想情况 在旧节点组中找新首。找到则将 DOM 移动到最前，且在旧节点组中设为 undefined；没找到则添加新元素到最前。
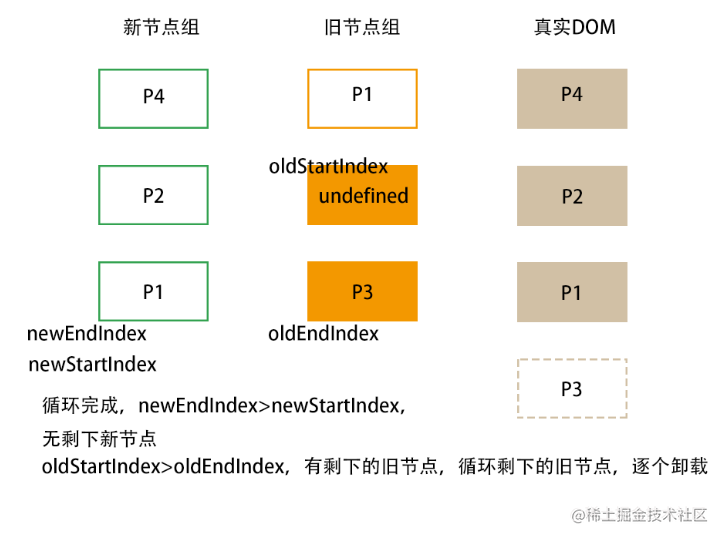
  2. 如果有新节点剩下，遍历剩下的新节点，挂载到当前旧节点组的头部节点。
  3. 如果有旧节点剩下，遍历剩下的旧节点，卸载。

# 流程图

# 准备工作

# 循环开始

# 循环完成，检查新增或者卸载

# 实现步骤

  • 定义 oldChildren 为 n1 的 children

  • 定义 newChildren 为 n2 的 children // 定义四个索引值

  • 定义 oldStartIndex 为 oldChildren 的首位索引值

  • 定义 oldEndIndex 为 oldChildren 的最后位索引值

  • 定义 newStartIndex 为 newChildren 的首位索引值

  • 定义 newEndIndex 为 newChildren 的最后位索引值 // 定义四个索引所对应的 VNode 节点

  • 定义 oldStartVNode 为 oldChildren[oldStartIndex]

  • 定义 oldEndVNode 为 oldChildren[oldEndIndex]

  • 定义 newStartVNode 为 newChildren[newStartIndex]

  • 定义 newEndVNode 为 newChildren[newEndIndex] // 进行比较

  • 循环？newStartIndex <= newEndIndex 且 oldStartIndex <= oldEndIndex

    1. oldStartVNode 不存在的话？ 说明该节点已经处理过了

      • 将 oldStartVNode 指向 oldChildren[++oldStartIndex]

    2. oldStartVNode.key === newStartVNode.key ?

      • 调用 patch(oldStartVNode,newStartVNode,container)打补丁
      • 将 oldStartVNode 指向 oldChildren[++oldStartIndex]
      • 将 newStartVNode 指向 newChildren[++newStartIndex]

    3. oldEndVNode.key === newEndVNode.key ?

      • 调用 patch(oldStartVNode, newStartVNode, container)打补丁
      • 将 oldEndVNode 指向 oldChildren[--oldEndIndex]
      • 将 newStartVNode 指向 newChildren [--newStartIndex]

    4. oldStartVNode.key === newEndVNode.key ?

      • 调用 patch(oldStartVNode, newEndVNode, container )打补丁
      • 调用 insert(oldStartVNode.el ,container ,oldEndVNode.el.nextSiling ) 将 oldStartVNode 移动到 oldEndVNode的下一个节点 前
      • 将 oldStartVNode 指向 oldChildren [ ++oldStartIndex ]
      • 将 newEndVNode 指向 newChildren[ --newEndIndex ]

    5. oldEndVNode.key === newStartVNode.key ?

      • 调用 patch( oldEndVNode, newStartVNode , container )打补丁
      • 调用 insert ( oldEndVNode.el , container , oldStartVNode.el ) 将 oldEndVNode 移动到 oldStartVNode 前
      • 将 oldEndVNode 指向 oldChildren [ --oldEndIndex ]
      • 将 newStartVNode 指向 newChildren[ ++newStartIndex ]

    6. 以上都不满足

      • 定义 idxInOld , 遍历 oldChildren ，找是否有和 newStartVNode 相同的 key ?
      • idxInOld > 0 在 oldChildren 中找到和 newStartVNode 相同的 key
        • 定义 vnodeToMove 为 oldChildren[idxInOld]
        • 调用 patch( vnodeToMove, newStartVNode , container )打补丁
        • 调用 insert ( vnodeToMove.el , container , oldStartVNode.el ) 将 vnodeToMove 移动到 oldStartVNode 前
        • 将 oldChildren[idxInOld] 设置为 undefined
      • idxInOld < 0 没有找到
        • 调用 patch(null,newStartVNode,container,oldStartVNode.el), 添加 newStartVNode
        • 将 newStartVNode 指向 newChildren[ ++newStartIndex ]

  • oldEndIndex < oldStartIndex && newEndIndex <= newStartIndex 检查索引的情况，看是否有需要新增的节点

    • 循环剩下的新节点 然后调用 patch(null,newChildren[i],container,oldStartVNode.el) 新增到 oldStartVNode 前

  • newEndIndex < newStartIndex && oldEndIndex >= oldStartIndex 检查是否有需要删除的节点

    • 循环剩下的旧节点，然后调用 unmount(oldChildren[i])

# 总结

双端diff算法指的就是在新旧两组节点的四个端点分别进行比较，并试图找到可用节点。相比较简单diff算法 (opens new window)，同样的场景下，DOM移动次数更少。